Data Forecasting Math Running

Hierarchical Machine Learning Classification Tasks

May 12th, 2020

Machine learning models have varying levels of accuracy which needs to be accounted for in production environments. By using a threshold-constrained hierarchy, we can make predictions based on membership probability to subsets of classes.

Home Projects

Overview🔗

Trained machine learning models are rarely 100% accurate when making predictions in any real-world task. This post describes the steps/tradeoffs that I took to minimize the number of mistakes that are made by a machine learning classifier and to maximize the utility of the classifier. This method can be used when stakeholders have a low-tolerance for errors in the domain of the machine learning classification. This method involves creating a class taxonomy, and creating thresholds at which a classification can be assigned or acted upon. The taxonomy, in combination with action thresholds, allows the developer to optimize the balance the risk tolerance of the stakeholders with efficiency of the process. By setting a higher confidence threshold for acting on a classification, fewer actions are taken but the actions that are taken should tend to be accurate. If the the threshold for action is lower, more actions will be taken, but the classifications may not be accurate.

Taxonomy🔗

The simplest machine learning classification tasks involve directly classifying samples into classes. This approach to classification relies exclusively on the ability of the model to identify the class of the sample. Many situations can involve classifying samples into one of hundreds or thousands of classes which can be difficult for these flat machine learning models to accurately predict. But making actionable predictions does not always require being able to classify samples into a specific class, but instead being able to determine if the samples are a member of any of a subset of classes that are similar. If a subset of those classes are similar in ways that can be acted on, they can be thought of as the same class. That subset of classes are said to form a higher level class. Higher level classes can be merged into even higher level classes, creating multiple layers of classes. In the context of hierarchical classification, these layers of classes are called a taxonomy of classes. Those classes from which all higher level classes are derived from are called leaf classes, in that they are the lowest and most specific classes in the taxonomy.

The taxonomy of classes allows action to be taken on these higher level classifications, even in the absence of good leaf classifications. For example, if we were trying to classify images of animals, the model may not accurately differentiate between a mountain lion and a house cat. However, depending on what our model is being used for, being able to identify the animal as a feline or as a mammal may be all that is needed to act on the data. If a flat approach were used, the model may end up providing falsely identifying the house cat as a mountain lion, resulting in only inaccurate information. But if a hierarchical classification approach were used, the model could still accurately label the animal as a mammal and a feline, even if the species is still wrong.

Taxonomies are often structured as trees, where lower-level classes are in a direct subset of one higher level class, but they can also be structured as Directed Acyclic Graphs (DAGs), where they are in the direct subset of multiple higher-level graphs. DAGs offer more flexibility and options for structuring higher-level classes, but makes making predictions much more difficult. I would recommend sticking to trees when first starting to work with hierarchical classification.

In a situation with low margin for error, a neural network was being applied using a flat classification classification where it was yielding low accuracy. By refactoring the prediction process into a hierarchical classification approach using the global classifier, actionable predictions increases by 35% by creating a taxonomy of classes which could be used to route information throughout the departments. The taxonomy used was structured similarly to the taxonomy below:

Below is the full Python code for loading, saving, constructing, and traversing our classification taxonomy:

import logging
import json
import collections
import requests


logger = logging.getLogger(__name__)


class AdjacencyList(object):

    def __init__(self, root, **lists):
        self.root = root
        self.data = lists

    def __repr__(self):
        output = ''
        for parent, children in self.data.items():
            output += '%r : %r\n' % (parent, children)
        return output

    def __contains__(self, item):
        return item in self.data

    def __len__(self):
        return len(self.data)

    def __iter__(self):
        for node in self.bfs():
            yield node

    def __getitem__(self, item):
        return self.data[item]

    def __setitem__(self, key, value):
        self.data[key] = value

    def dfs(self, **kwargs):
        """
        Runs a depth-first search over the AdjacencyList

        args:
            root (object):  The node to consider the root of the tree, defaults to the top-level root node

        yields:
            object: node
        """
        root = kwargs.get('root', self.root)
        if root not in self.data:
            raise ValueError('%r not in adjacency list' % root)
        nodes = [root]
        while nodes:
            node = nodes.pop()
            if node in self.data:
                nodes += self.data[node]
            yield node

    def bfs(self, **kwargs):
        """
        Runs a breadth-first search over the AdjacencyList

        args:
            root (object):  The node to consider the root of the tree, defaults to the top-level root node

        yields:
            object: node
        """
        root = kwargs.get('root', self.root)
        if root not in self.data:
            raise ValueError('%r not in adjacency list' % root)
        nodes = [root]
        while nodes:
            node = nodes.pop(0)
            if node in self.data:
                nodes += self.data[node]
            yield node

    def add(self, parent, child):
        if parent not in self.data:
            self.data[parent] = []
        if child not in self.data:
            self.data[child] = []
        if child not in self.data[parent]:
            self.data[parent].append(child)
        if child == self.root:
            self.root = parent

    def remove(self, node):
        """
        Removes a node from the AdjacencyList

        args:
            node (object):  The node to be removed from the tree

        Raises:
            ValueError: The node does not exist in the tree
        """
        if node not in self.data:
            raise ValueError('%r not in adjacency list' % node)
        if node == self.root and len(self.data[node]) > 1:
            raise ValueError('Removing root(%s) with result in multiple root nodes(%r)' % (node, self.data[node]))
        elif node == self.root and len(self.data[node]) == 1:
            self.root = self.data[node][0]
        self.data.pop(node)
        for parent, children in self.data.items():
            if node in children:
                self.data[parent].remove(node)

    def parent(self, node):
        """
        Returns the parent of a node

        args:
            node (object):  The node for which to get the parent

        Returns:
            object: the parent of node

        Raises:
            ValueError: The node does not exist in the tree, or does not have a parent
        """
        if node not in self.data:
            raise ValueError('%r is not a node' % node)
        for parent, children in self.data.items():
            if node in children:
                return parent
        raise ValueError('node(%r) does not have a parent in %r' % (node, self))

    def branches(self):
        """
        Returns the nodes in the AdjacencyList that have children

        Returns:
            list: nodes in the tree that have children
        """
        return [node for node in self.data.keys() if self.children(node)]

    def leaves(self):
        """
        Returns the nodes in the AdjacencyList that do not have children

        Returns:
            list: nodes in the tree that do not have children
        """
        return [node for node in self.data.keys() if not self.children(node)]

    def ancestors(self, node):
        """
        Returns  ancestors of a node

        args:
            node (object): The node for which to get ancestors

        Returns:
            list: ancestors of the given node (sorted from oldest to youngest)
        """
        if node not in self.data:
            raise ValueError('%r not in adjacency list' % node)
        parent = node
        ancestors = []
        while parent != self.root:
            parent = self.parent(parent)
            ancestors = [parent] + ancestors
        return ancestors

    def children(self, node):
        """
        Returns the direct children of the node

        args:
            node (object): The node for which to fetch children

        Returns:
            list: children of the given node

        Raises:
            ValueError: node is not in the AdjacencyList
        """
        if node not in self.data:
            raise ValueError('%r not in adjacency list' % node)
        return self.data[node]

    def height(self):
        """
        Calculates the height of the AdjacencyList

        Returns:
            int: The height of the AdjacencyList
        """
        node_queue = [self.root]
        height = 0
        while True:
            node_count = len(node_queue)
            if not node_count:
                return height
            height += 1
            while node_count:
                node = node_queue.pop(0)
                children = self.data[node]
                node_queue += children
                node_count -= len(children)

    def lowest_common_ancestor(self, *nodes):
        """
        Calculates the lowest common ancestor of the given nodes

        Returns:
            object: The lowest ancestor in AdjacencyList that has all the specified nodes as a descendant
        """
        if all(node == nodes[0] for node in nodes):
            return nodes[0]
        node_ancestors = [self.ancestors(node) + [node] for node in nodes]
        current_common_ancestor = None
        for generation in zip(*node_ancestors):
            if all(node == generation[0] for node in generation):
                current_common_ancestor = generation[0]
        return current_common_ancestor

    def to_dict(self):
        """
        Converts the AdjacencyList to a dictionary

        Returns:
            dict
        """
        dictionary = dict(root=self.root, data=self.data)
        return dictionary

    def save(self, file_name):
        """
        Saves AdjacencyList to a file

        args:
            file_name (str): The file name to save the AdjacencyList to
        """
        data = self.to_dict()
        with open(file_name, 'w') as output_file:
            json.dump(data, output_file)

    @classmethod
    def from_dict(cls, root, data):
        """
        Construct an AdjacencyList instance from a dictionary

        args:
            root (object): The root node of the AdjacencyList
            data (dict): The parent-children dictionary of the nodes in the AdjacencyList

        Returns:
            AdjacencyList

        Raises:
            ValueError - Some nodes are not hashable, tree contains loops
        """
        for key, values in data.items():
            values = list(values)
            if any(not isinstance(value, collections.Hashable) for value in values):
                raise ValueError('all children of %r must be hashable(%r)' % (key, values))
            if key in values:
                raise ValueError('tree cannot have any loops (%r -> %r)' % (key, key))
            data[key] = values
            for value in values:
                if value not in data:
                    data[value] = []
        return cls(root, **data)

    @classmethod
    def load(cls, file_name):
        """
        Loads AdjacencyList instance from file_name

        args:
            file_name (str): The file_name containing the AdjacencyList data

        Returns:
            AdjacencyList
        """
        with open(file_name, 'r') as input_file:
            data = json.load(input_file)
        root = data['root']
        data = data['data']
        return cls.from_dict(root, data)

But after creating our hierarchy, our process was still assigning inaccurate leaf classes in addition to our accurate higher-level classes. I decided to move away from this mandatory lead-node prediction (MLNP) and move towards non-mandatory leaf-node prediction (NMLNP), where the hierarchical classifier is not required to return a leaf node as the prediction. To systematically limit assigning inaccurate classes, I added thresholds for node prediction assignments, by classifying samples to the lowest ancestor in the taxonomy which exceeds the threshold. By creating this taxonomy of classifications relating to our machine learning model, action can still be taken on samples that the model could not verify with a high degree of certainty.

Putting it all Together🔗

We compute the probabilities of these parent classifications by summing the probabilities of the immediate children of a parent classification. If this computed probability is greater than the threshold, we classify the sample to that parent classification, as it is the lowest classification in the taxonomy that exceeds our threshold. If not, we look at the parent of that classification, and perform the same calculations and comparison to the threshold. If we continue this process until we get to the root classification without exceeding a threshold we do not classify the sample at all.

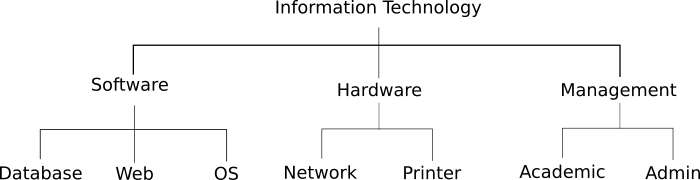
In the below example, the machine learning classifier did not produce predictions that exceeded any of the classifications (.0.70), so we sum the probabilities for the child classifications of each parent, and assign that value as the probability for that parent. We then compare the parent probabilities to the threshold, and find that the sample can be assigned to “Hardware”, which exceed the threshold. If no parent probability exceeded the threshold, we would not take any action, as the parent of the Software, Hardware, and Management classifications is the root of the taxonomy.

Let’s examine the code that will handle these threshold comparisons, and traversal of our hierarchy.

import logging
import collections


logger = logging.getLogger(__name__)


class HierarchicalClassifier(object):
    """
    Creates a classifier that will classify data into labels in a hierarchy
    If a threshold is provided, will only assign a label to data if the score is
    is above the specified threshold.  How the score is determined depends on the
    estimator used

    args:
        class_hierarchy (hierarchy.AdjacencyList): The tree of labels that can be assigned to data samples.  The HierarchicalClassifier will make predictions from the root label moving down the tree
    """

    def __init__(self, class_hierarchy, **kwargs):
        self.class_hierarchy = class_hierarchy

    def threshold(self, y, **kwargs):
        """
        Predicts the hierarchical labels for data samples

        Returns the lowest node in the hierarchy that exceeds the given threshold in the class_hierarchy.
        

        args:
            y (list of dict): List of dictionaries, consisting of the label-probabilities of each label.  Each label must be in the class_hierarchy

        Keyword Arguments:
            threshold (float): The threshold probability for classifying a sample as a given label, defaults to negative infinity.
            hierarchy (bool): Determines if an ordered list of ancestor labels should be returned for each sample instead of the lowest label in the class hierarchy.  Defaults to False.

        Returns:
            list: if hierarchy=False, classes corresponding to the provided data samples.  If hierarchy=True, lists of ancestor labels of the predicted label in the class hierarchy

        Raises:
            ValueError:  Raised if a label is encountered that is not found in the class_hierarchy
        """
        threshold = kwargs.get('threshold', float('-inf'))
        if isinstance(threshold, dict):
            default_threshold = threshold.get('default', float('-inf'))
        elif isinstance(threshold, (float, int)):
            default_threshold = float(threshold)
            threshold = dict()
        else:
            threshold = dict()
            default_threshold = float('-inf')
        unique_labels = [item['name'] for item in y[0]]
        hierarchy = kwargs.get('hierarchy', False)
        leaf_class_ancestors = dict((leaf, self.class_hierarchy.ancestors(leaf) + [leaf]) for leaf in unique_labels)

        leaf_probabilities = []
        for predictions in y:
            leaf_probability = dict()
            for prediction in predictions:
                leaf_probability[prediction['name']] = prediction['probability']
            leaf_probabilities.append(leaf_probability)
        outputs = []

        for sample in leaf_probabilities:
            sample_predictions = dict()
            for leaf, probability in sample.items():
                for ancestor in leaf_class_ancestors[leaf]:
                    if ancestor in sample_predictions:
                        sample_predictions[ancestor] += probability
                    else:
                        sample_predictions[ancestor] = probability

            leaf_prediction = max(sample, key=sample.get)
            sample_hierarchy = []
            for index, ancestor in enumerate(leaf_class_ancestors[leaf_prediction]):
                if threshold is not None:
                    # fetch the branch-specific threshold, falls back to the default threshold
                    ancestor_threshold = threshold.get(ancestor, default_threshold)

                    if ancestor == self.class_hierarchy.root or not kwargs.get('normalize', False):
                        parent_ancestor_probability = 1.0
                    else:
                        parent_ancestor = leaf_class_ancestors[leaf_prediction][index - 1]
                        parent_ancestor_probability = sample_predictions[parent_ancestor]
                    ancestor_probability = sample_predictions[ancestor] / parent_ancestor_probability
                    if (self.leaf and ancestor_probability >= ancestor_threshold) or parent_ancestor_probability >= threshold.get(parent_ancestor, default_threshold):
                        current_label = ancestor
                else:
                    current_label = ancestor
                if hierarchy:
                    sample_hierarchy.append(current_label)

            if hierarchy:
                outputs.append(sample_hierarchy)
            else:
                outputs.append(current_label)
        return outputs

    def evaluate(self, y_true, y_pred, **kwargs):
        """
        Provides classification reports for each level in the hierarchy.  If a threshold is provided, the top-level report will contain the root label to denote data samples that could not be predicted with a confidence above the threshold

        args:
            y_true (list): The correct labels for the data
            y_predicted (list): The labels predicted by the HierarchicalClassifier

        Returns:
            dict: classification reports for the children of each parent in the hierarchy that were included in y_true or y_predicted
        """
        from sklearn import metrics
        kwargs.setdefault('recurse', True)
        root = kwargs.get('root', self.class_hierarchy.root)
        # remove datapoints with None predictions
        parent_data = dict((parent, dict(labels=[], predictions=[])) for parent in self.class_hierarchy.branches())
        # create the datasets for each parent with one iteration

        for label, prediction in zip(y_true, y_pred):
            if prediction == root:
                continue
            prediction_ancestors = self.class_hierarchy.ancestors(prediction) + [prediction]
            label_ancestors = self.class_hierarchy.ancestors(label) + [label]
            for index, (label_ancestor, prediction_ancestor) in enumerate(zip(label_ancestors[1:], prediction_ancestors[1:])):
                if label_ancestors[index] != prediction_ancestors[index]:
                    continue
                parent_data[label_ancestors[index]]['labels'].append(label_ancestor)
                parent_data[label_ancestors[index]]['predictions'].append(prediction_ancestor)
        reports = dict()
        for parent in self.class_hierarchy.branches():
            current_labels = parent_data[parent]['labels']
            current_predictions = parent_data[parent]['predictions']
            if not current_labels or not current_predictions:
                continue
            logger.debug('Creating classification_report for %r', parent)
            reports[parent] = metrics.classification_report(current_labels, current_predictions)
        return reports

    def score(self, y_pred, y, **kwargs):
        """
        Provides score (0 - 1) of the HierarchicalClassifier for each parent in the hierarchy

        args:
            X (list): Data samples to use to score the classifier
            y (list): Data labels to use to score the classifier

        Returns:
            dict: scores for all parents in the hierarchy that had children in y
        """
        kwargs.setdefault('recurse', True)
        root = kwargs.get('root', self.class_hierarchy.root)
        # remove datapoints with None predictions
        parent_data = dict((parent, dict(labels=[], predictions=[])) for parent in self.class_hierarchy.branches())
        # create the datasets for each parent with one iteration
        for label, prediction in zip(y, y_pred):
            if prediction == root:
                continue
            prediction_ancestors = self.class_hierarchy.ancestors(prediction) + [prediction]
            label_ancestors = self.class_hierarchy.ancestors(label) + [label]
            for index, (label_ancestor, prediction_ancestor) in enumerate(zip(label_ancestors[1:], prediction_ancestors[1:])):
                if label_ancestors[index] != prediction_ancestors[index]:
                    continue
                parent_data[label_ancestors[index]]['labels'].append(label_ancestor)
                parent_data[label_ancestors[index]]['predictions'].append(prediction_ancestor)

        scores = dict()
        for parent in self.class_hierarchy.branches():
            current_labels = parent_data[parent]['labels']
            if not current_labels:
                continue
            current_predictions = parent_data[parent]['predictions']
            label_count = len(current_labels)
            correct_predictions = sum(1 for prediction, label in zip(current_predictions, current_labels) if prediction == label)
            score = correct_predictions / float(label_count)
            scores[parent] = score
        return scores

Let’s show an example of how you might use this HierarchicalClassifierin a real-world scenario:

from hierarchy import AdjacencyList, HierarchicalClassifier

raw_class_hierarchy = {
	"data": {
		"Information Technology": ["Hardware", "Management", "Software"],
		"Hardware": ["Network", "Printer"],
		"Management": ["Academic", "Admin"],
		"Software": ["Database", "OS", "Web"]
	},
	"root": "Information Technology"
}


hierarchy = AdjacencyList.from_dict(raw_class_hierarchy)
hclf = HierarchicalClassifier(hierarchy)
...
for sample in samples:
    sample_predictions = [
        {
            "Database": 0.0752,
            "OS": 0.08,
            "Web": 0.22,
            "Network": 0.45,
            "Printer": 0.18,
            "Academic": 0.0045,
            "Admin": 0.003
        },
        {
            "Database": 0.01,
            "OS": 0.3,
            "Web": 0.0,
            "Network": 0.091,
            "Printer": 0.05,
            "Academic": 0.0,
            "Admin": 0.0
        },
        {
            "Database": 0.15,
            "OS": 0.15,
            "Web": 0.15,
            "Network": 0.15,
            "Printer": 0.15,
            "Academic": 0.15,
            "Admin": 0.10
        }
    ]
    hierarchical_prediction =  hclf.threshold(sample_predictions, threshold=0.60)
    print(hierarchical_prediction)  # ["Software", "Network", "Information Technology"]

The HierarchicalClassifier` has a few benefits:

• Reusability: the HierarchicalClassifierdoes not interact directly with the model, only the output probabilities. It can be used with any machine learning framework, any neural network architecture, or any set of labeled probabilities.
• Taxonomy agnostic: The implementation will work with any taxonomy containing the classes predicted by the classifier, so the number of layers in the taxonomy will not make a difference when making classifications. This also means that the same classifier can be used in multiple hierarchies, allowing developers to swap hierarchies in/out of the implementation at runtime.
• Dynamic: This implementation allows hierarchies to built and altered at runtime, so the developer can use other techniques to dynamically build the optimal taxonomy from a database, or restructure the taxonomy to meet the needs of their situation. It also allows for developers to build interfaces for non-technical stakeholders to build/modify the taxonomy and thresholds without developers.

UPDATE: After implementing this code (and this post) I discovered that there was already a whole field of study dedicated to this problem. I went ahead and updated this post to reflect the language used in that research. If you are interested in diving deeper into methods of hierarchical classification, I would recommend A survey of hierarchical classification across different application domains to get a high level overview of hierarchical classification techniques and advantages/disadvantages to each.